Math Models Worksheet 4.1 Relations and Functions Answers

Math Models Worksheet 4.1 Relations and Functions Answers: Understanding the Basics

Are you struggling to understand relations and functions in math? Look no further than the Math Models Worksheet 4.1 Relations and Functions Answers. This worksheet is designed to help you understand the fundamentals of relations and functions in an interactive and engaging way. Let’s dive in and explore what this worksheet has to offer.

Understanding Relations and Functions

Before we get into the specific answers of the worksheet, let’s review what relations and functions are in math. A relation is simply a set of ordered pairs, while a function is a relation where each input has exactly one output. In other words, a function is a special kind of relation where every input corresponds to exactly one output.

For example, let’s consider the relation {(1,2), (3,4), (5,6)}. This is a relation because it is a set of ordered pairs. However, it is not a function because the input 1 corresponds to the output 2, but the input 3 also corresponds to the output 4. Therefore, it is not a function because one input has multiple outputs.

On the other hand, the relation {(1,2), (3,4), (5,6)} can be made into a function by taking only the first element of each ordered pair as the input and the second element as the output. In this case, the function would be f(x) = x + 1.

Solving Problems with Math Models Worksheet 4.1 Relations and Functions Answers

Now that we have a better understanding of what relations and functions are, let’s explore the types of problems that the Math Models Worksheet 4.1 Relations and Functions Answers can help you solve.

One common problem in relation and function is determining if a relation is a function. To do this, you need to check if every input has exactly one output. If there is one input that has multiple outputs, then the relation is not a function.

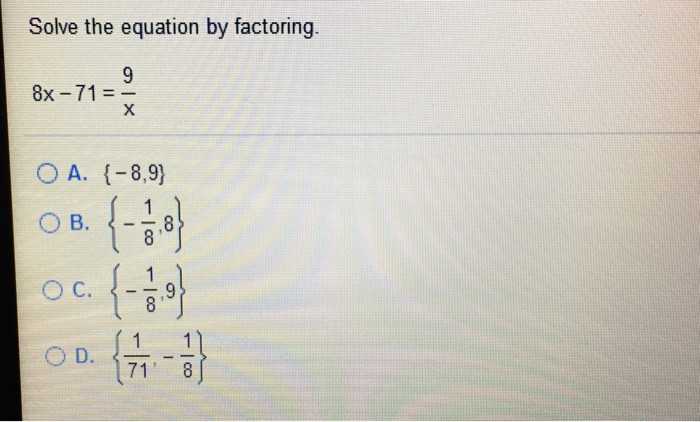
Another problem involves finding the domain and range of a function. The domain is the set of all possible inputs, while the range is the set of all possible outputs. To find the domain and range of a function, you need to look at the inputs and outputs and determine what values they can take on.

Lastly, the worksheet can help you solve problems involving function notation. Function notation is simply a way of writing a function using f(x) instead of y. For example, instead of writing y = x + 1, you can write f(x) = x + 1.

Conclusion

In summary, the Math Models Worksheet 4.1 Relations and Functions Answers is a valuable resource for understanding the basics of relations and functions in math. By practicing with this worksheet, you can improve your skills in determining if a relation is a function, finding the domain and range of a function, and using function notation. So why not give it a try and see how it can help you in your math studies?

If you’re looking for help with Math Models Worksheet 4.1 Relations and Functions Answers, you’ve come to the right place. This worksheet can be a bit tricky, but with a little guidance and practice, you’ll be solving functions like a pro in no time.

First, let’s review what we mean by relations and functions. In math, a relation is simply a set of ordered pairs, while a function is a special type of relation where each input (or x-value) corresponds to exactly one output (or y-value). This means that for every x-value in a function, there is only one possible y-value.

Now let’s take a look at some of the problems on the worksheet. One question might ask you to determine whether a given set of ordered pairs is a function or not. To do this, you’ll need to check if there are any repeated x-values. If there are, then the set is not a function because one x-value corresponds to more than one y-value. If there are no repeated x-values, then the set is a function.

Another type of problem might ask you to find the domain or range of a given function. The domain of a function is simply the set of all possible x-values, while the range is the set of all possible y-values. To find the domain, you’ll need to look at all the possible x-values that make sense for the function. For example, if you’re dealing with a function that represents the height of a bouncing ball, the domain might be limited to positive values (since you can’t have negative time). To find the range, you’ll need to look at all the possible y-values that the function can output.

One common technique for solving functions is to use function notation. Instead of writing out “y =” every time, we can simply use f(x) to represent the output for a given input. For example, if we have a function that represents the cost of a movie ticket based on the number of tickets purchased, we could write f(x) = 10x to represent the cost of x tickets.

Finally, it’s important to remember that functions can be represented in different ways, including algebraically, graphically, and through tables of values. Each representation has its own advantages and disadvantages, so it’s important to be comfortable with all three.

In summary, Math Models Worksheet 4.1 Relations and Functions Answers can be challenging, but by understanding the concepts of relations, functions, domain, range, and function notation, you’ll be well on your way to solving these problems with ease. Practice makes perfect, so keep working at it and don’t be afraid to ask for help if you need it.