Graphing A Parabola From Vertex Form Worksheet Answer Key: Your Guide to Mastering Quadratic Functions
Are you struggling with graphing parabolas in vertex form? Don’t worry, you’re not alone. Many students find this topic challenging, but with practice and the right resources, you can master it. One such resource is the Graphing A Parabola From Vertex Form Worksheet. In this article, we’ll take a closer look at this worksheet, including what it is, how to use it, and why it’s helpful for mastering quadratic functions.
What is Graphing A Parabola From Vertex Form Worksheet?
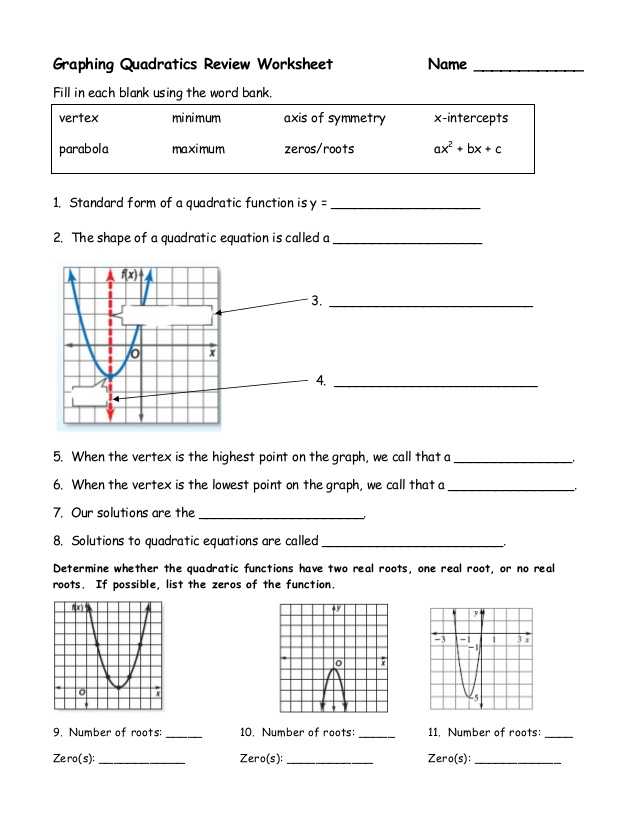
Graphing A Parabola From Vertex Form Worksheet is a practice sheet designed to help students understand and master the concept of graphing parabolas in vertex form. The worksheet includes several questions that require students to apply their knowledge of quadratic functions, including finding the vertex, axis of symmetry, and intercepts of the graph.
How to Use Graphing A Parabola From Vertex Form Worksheet Answer Key
To use the Graphing A Parabola From Vertex Form Worksheet Answer Key, start by reviewing the concept of quadratic functions and vertex form. Make sure you understand the standard form of a parabola, which is y = ax^2 + bx + c. Then, familiarize yourself with the vertex form, which is y = a(x – h)^2 + k, where (h, k) is the vertex of the parabola.
Once you’ve reviewed these concepts, you can start working through the worksheet. The answer key provides solutions to all of the questions, so you can check your work as you go. Make sure to show your work and check each step carefully to avoid mistakes.
Why is Graphing A Parabola From Vertex Form Worksheet Answer Key helpful?
The Graphing A Parabola From Vertex Form Worksheet Answer Key is a helpful resource for several reasons. Firstly, it provides practice problems that are similar to those that you may encounter on a test or exam. By working through these problems, you can strengthen your understanding of quadratic functions and improve your problem-solving skills.
Secondly, the answer key allows you to check your work and identify any mistakes you may have made. This is essential for learning and improvement, as it helps you identify areas where you need to focus more attention and practice.

Finally, the worksheet can be a useful study tool when preparing for a test or exam. By working through the problems and checking your answers, you can identify areas where you need to review further and feel more confident in your abilities.
Conclusion
Graphing A Parabola From Vertex Form Worksheet Answer Key is a valuable resource for any student looking to master quadratic functions. By using this worksheet, you can strengthen your understanding of parabolas in vertex form, improve your problem-solving skills, and prepare for tests and exams. So, don’t hesitate to download and use this worksheet to help you achieve success in your math studies.
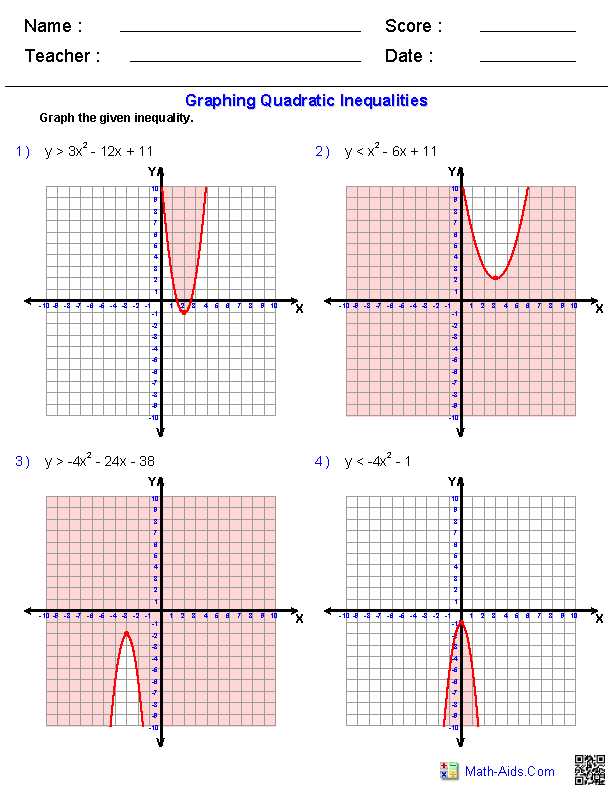
Now that you have a good understanding of what a parabola is and how it can be graphed in standard form, let’s take a closer look at how to graph a parabola from vertex form using the Graphing A Parabola From Vertex Form Worksheet Answer Key.
Vertex form is a way of expressing a quadratic equation in terms of its vertex, or the point where the parabola intersects its axis of symmetry. The general form of a quadratic equation in vertex form is y = a(x – h)^2 + k, where (h, k) is the vertex of the parabola.
To graph a parabola from vertex form, you can follow a few simple steps:
Step 1: Identify the vertex
The first step is to identify the vertex of the parabola. In vertex form, the vertex is given by (h, k), where h is the x-coordinate of the vertex and k is the y-coordinate of the vertex. The vertex is the highest or lowest point of the parabola, depending on whether the leading coefficient a is positive or negative.
Step 2: Identify the axis of symmetry
The axis of symmetry is a vertical line that passes through the vertex of the parabola. In vertex form, the equation of the axis of symmetry is x = h.
Step 3: Determine the direction of opening
The direction of opening of the parabola is determined by the sign of the leading coefficient a. If a is positive, the parabola opens upward, and if a is negative, the parabola opens downward.
Step 4: Plot additional points
To graph the parabola, you can plot additional points on either side of the vertex. One convenient method for doing this is to use the symmetry of the parabola. Because the parabola is symmetric about its axis, you can find the y-coordinate of any point on the parabola by reflecting a point with the same x-coordinate across the axis.
Step 5: Draw the parabola
Using the points you have plotted, you can draw the parabola. Make sure to draw a smooth curve that passes through all of the points.
The Graphing A Parabola From Vertex Form Worksheet Answer Key provides practice problems and answers for each step of this process. By working through the worksheet, you can develop your understanding of how to graph a parabola from vertex form and get valuable practice with the process.
In summary, graphing a parabola from vertex form involves identifying the vertex, axis of symmetry, and direction of opening, plotting additional points, and drawing the parabola. By using the Graphing A Parabola From Vertex Form Worksheet Answer Key, you can get practice with this process and improve your skills in graphing parabolas.