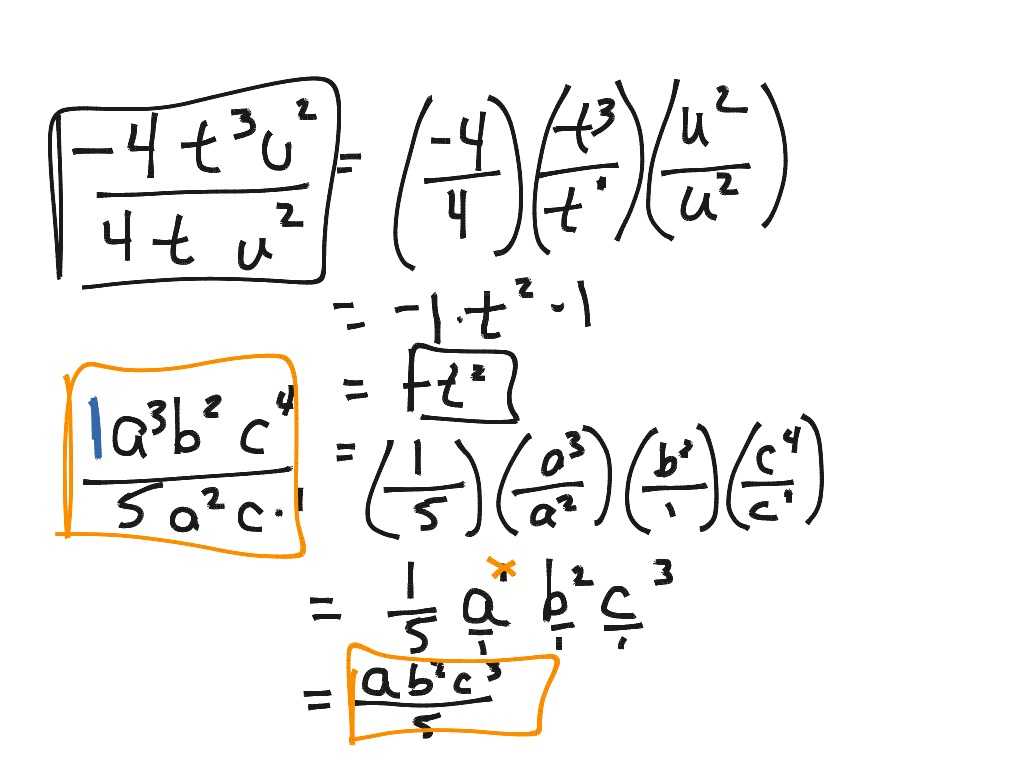Probability with A Deck Of Cards worksheets are a great way to learn and practice math skills. While you might think that learning how to figure the probability with a deck of cards is as easy as flipping a coin, the reality is that there are more steps involved than simply flipping a coin. Many times, cards can also fall out of your deck, and you will need to determine how many cards remained in the deck.
You will need to understand the probabilities of each card having an exact number of spots or card spots on each face. You will also need to know how many of each spot are covered. Knowing the cards that are on each face is called a “deck” of cards. This will help you determine how many of each card you have.

Once you know how many cards are on each face, you will need to know how many are in the deck. In a standard deck of cards, there are fifty-two cards. This means there are two five-card spaces. Therefore, if there are two cards remaining in the deck, you will need to know how many cards are left in the deck.
When you take the probabilities of each card, you will find that there are about two percent chance of each card coming up heads, and about one percent chance of each card coming up tails. Once you have these probabilities, you will be able to calculate the probability of each card coming up heads and the probability of each card coming up tails. You can then multiply these results together to find the total probability of the event happening.
If there are two cards remaining in the deck, then there is a twenty-five percent chance that there are two left in the deck. If you multiply this figure by the one percent probability of the event happening, then you will find that the probability is twenty-five times the one percent value. This will help you determine how many of each card remain in the deck. In addition, you will need to know how many cards remain from the bottom of the deck.
Suppose you have chosen a sample case, and that there are three left in the deck. The probability of all three cards remaining in the deck is about twenty-three times the one-percent probability of the event happening. Multiply this figure by the twenty-five percent value, and you will find that the probability is twenty-three times the total probability of the event happening.

Again, in the sample case, the probability of all three cards remaining in the deck is twenty-three times the total probability of the event happening. This means that you have a forty-four percent chance of winning the game. Therefore, your odds are approximately one in three. Keep this example in mind when learning how to figure out the probabilities of each card, and you will find that the probabilities will vary from situation to situation.
Learn to interpret the figures, and you will be able to apply it to all types of situations and scenarios. The secret to solving problems with probabilities is to remember that there are many factors involved, and that these are subject to change.