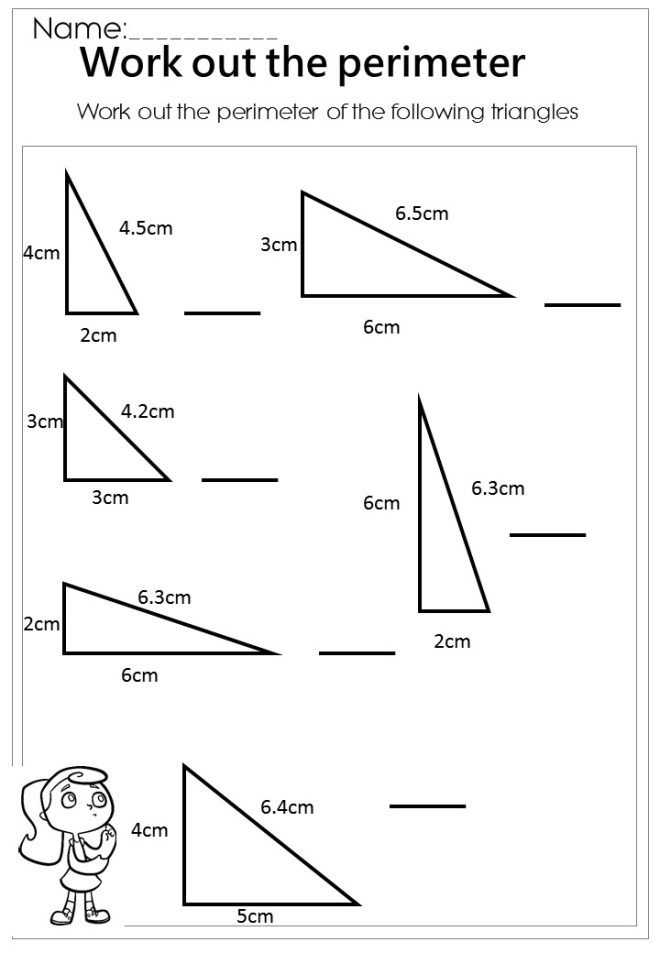
Have you ever wondered why a triangle always has three angles, and why in the US, we use the term “angles” when we mean “triangles”? I bet you did, but then you probably wondered, why is this so? And why should that be important?
What’s interesting about angles is that it relates to mathematical circles, something very simple to understand and is often misunderstood. Here’s the math: When you draw a circle, the length of the circle is a “unit” and the width is the “area”.
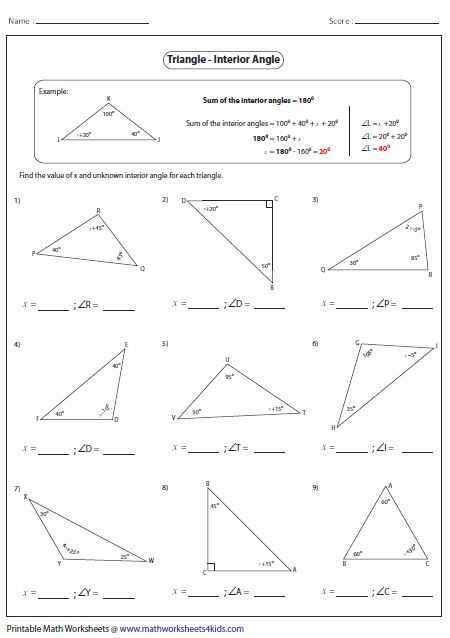
The same holds true for angles, with the same unit length and the same area. Now, let’s look at an example:
If you draw a line from the origin (the centre) to the right hand end of the angle, you’ll see that the angle’s angle is a little less than 90 degrees. But if you draw a line from the origin (the centre) to the left hand end of the angle, you’ll see that the angle’s angle is a little more than 90 degrees. So, if you divide the angle’s angle by the square root of the side length, you get a value close to the angle’s reciprocal.
Now, what if you start at the origin and add a right angle to the part you started at (adding to the ‘total’ is ‘cosine’), and then add a left angle to the part you started at (adding to the ‘total’ is ‘sine’), you will get the angle’s reciprocal. So, by dividing the ‘total’ by the reciprocal, you will get the angle’s angle, again.
As you can see, a triangle has a ‘total’ side and a ‘reciprocal’ side. By dividing the reciprocal by the square root of the ‘total’, you will get the angle’s angle. So, that’s why we use the term “angles” for a triangle when we mean a circle. It relates to the way angles are used to define the ‘diameter’ of the circle’s perimeter, or area, which is related to the way angles are used to define the shape of the circle’s circumference, or diameter.
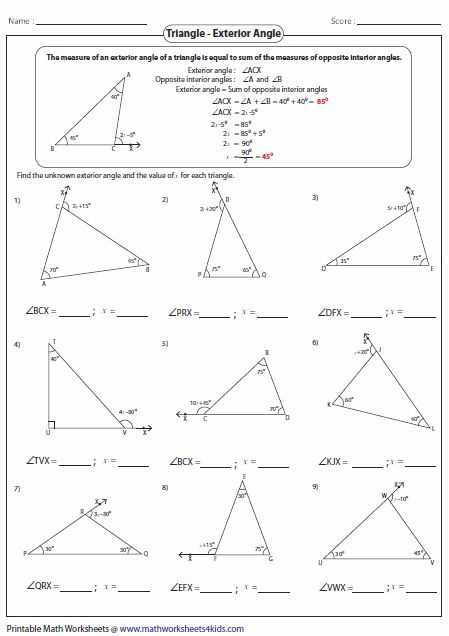
In fact, another name for the word “angles” is “quadrant”, as it relates to the shape of the ‘circle’s equator. So, maybe you should start looking for some ‘angles’ worksheets for your next projects. It can’t hurt, right? In any case, thanks for reading my article.