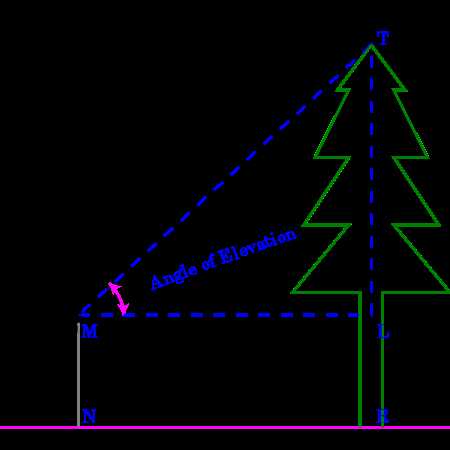
As you may know, there are many angles and declination terms to choose from when using trig. However, when dealing with topographical data, it is imperative that you understand both angles and depression terms, so you can better use the tools presented in your Angle of Elevation and Depression Trig Worksheet.
When studying topography, you should first consider the area on which you will be working. By studying areas of interest and determining what declination and angle are used, you will be in a better position to correctly create and interpret topographical data. This is important because there are several ways to divide a surface into different quadrants. Two quadrants, each defined by different angles of elevation, will be divided into four equal sections, each of which is divided by a line between quadrants and described by declination. Each quadrant of a given area is referred to as an angle, a quadrant, an angle, and so on.

The first quadrant of a point is referred to as the horizontal angle and represents the natural phenomenon of gravity acting on the earth. The second quadrant is the declination angle and is perpendicular to the horizontal. The third quadrant, then, is the depression angle and represents gravity acting against the perpendicular of the declination angle.
The fourth quadrant, the depression angle, is a natural phenomenon. Gravity does not act on the vertical angle of elevation and depression in the same way as it does on the horizontal angle. Instead, gravity always acts with an angle, a different angle than the horizontal angle of elevation and depression. A mathematical function known as the y-intercept can be written as the square root of two sides of the depression angle.
To find the intersection of two lines, the intersection of the horizontal angle and the depression angle will give you the intersection of the horizontal and vertical. In cases of highly skewed surfaces, the intersection of the depression angle and the vertical may be very difficult to determine, but a minimum of two points will often suffice. For instance, if you have two horizontal angles of elevation and depression, and the y-intercept is approximately two points ahead of one of the lines, the intersection of these two lines will give you the intersection of the lines.
The elevation angle is generally referred to as “north” and the depression angle as “south”. In cases where you are dealing with a very skewed surface, such as those found in many Native American ruins, it is very important that you know how to properly compare the angles of elevation and depression.

The diagonal angle of elevation and depression is referred to as the east-west line. This diagonal angle is directly opposite to the vertical and is perpendicular to the horizontal. Therefore, if you are to compare the angles of elevation and depression of the same horizontal line, you will need to define a straight line to be perpendicular to the depression angle.
Once you have defined the line that is perpendicular to the horizontal, you can convert the vertical angle that is in the form of a horizontal angle and convert it to a horizontal angle. You will need to convert the elevation angle that is written as “north” to the north line. Next, convert the depression angle that is written as “south” to the south line.