With practice worksheets, you can prove that a given function can be written in quadratic form. This is done by providing the exact values of the variables, if the complex variable is itself a quadratic equation. If a quadratic function has only one root, the variable gives the quadratic form of the function when it is plotted on a quadratic plot.
A quadratic function, if plotted in quadratic form, will have a unique shape. The shape and lines are important, as it lets you see exactly what the quadratic function is and how it will behave when plotted on a graph.
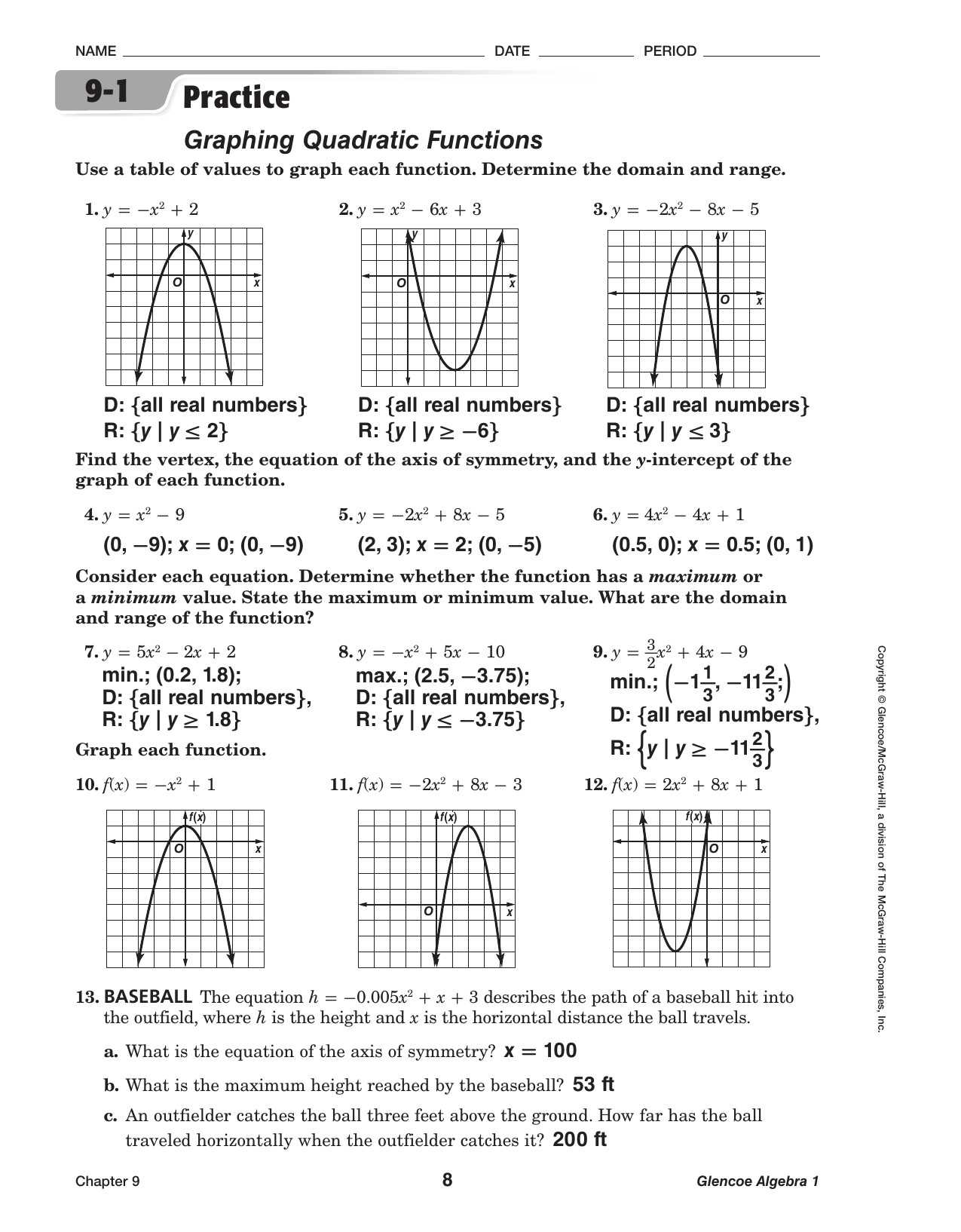
Quadratic functions are an important tool in many applications, such as optimization and linear algebra. Quadratic equation graphing enables us to get an idea of how a function changes as the value of the variable goes to zero. This is known as a quadratic equation. In order to prove that a given function can be written in quadratic form, you need to know what you are looking at.
Graphing quadratic functions is called graphing quadratic functions in standard form. You do not need to do any exact computations. Graphing quadratic functions is easy, even for a beginner, provided you have a good graphing program.
Quadratic functions are easy to plot, since they have only one root. They can be plotted without too much trouble, provided that you use standard mathematical procedures. The easiest way to create a quadratic function is to find a graph of a triangle in the vertical plane. Add a constant, called the “I” in this graph, to every point on the triangle and choose the first integer and place it at the origin.
After you find the first point, add the point to the origin and repeat this process until you have all the points. Now you know how many angels there are between any two points. Use these angles to find the slope of the line connecting the origin and each point.
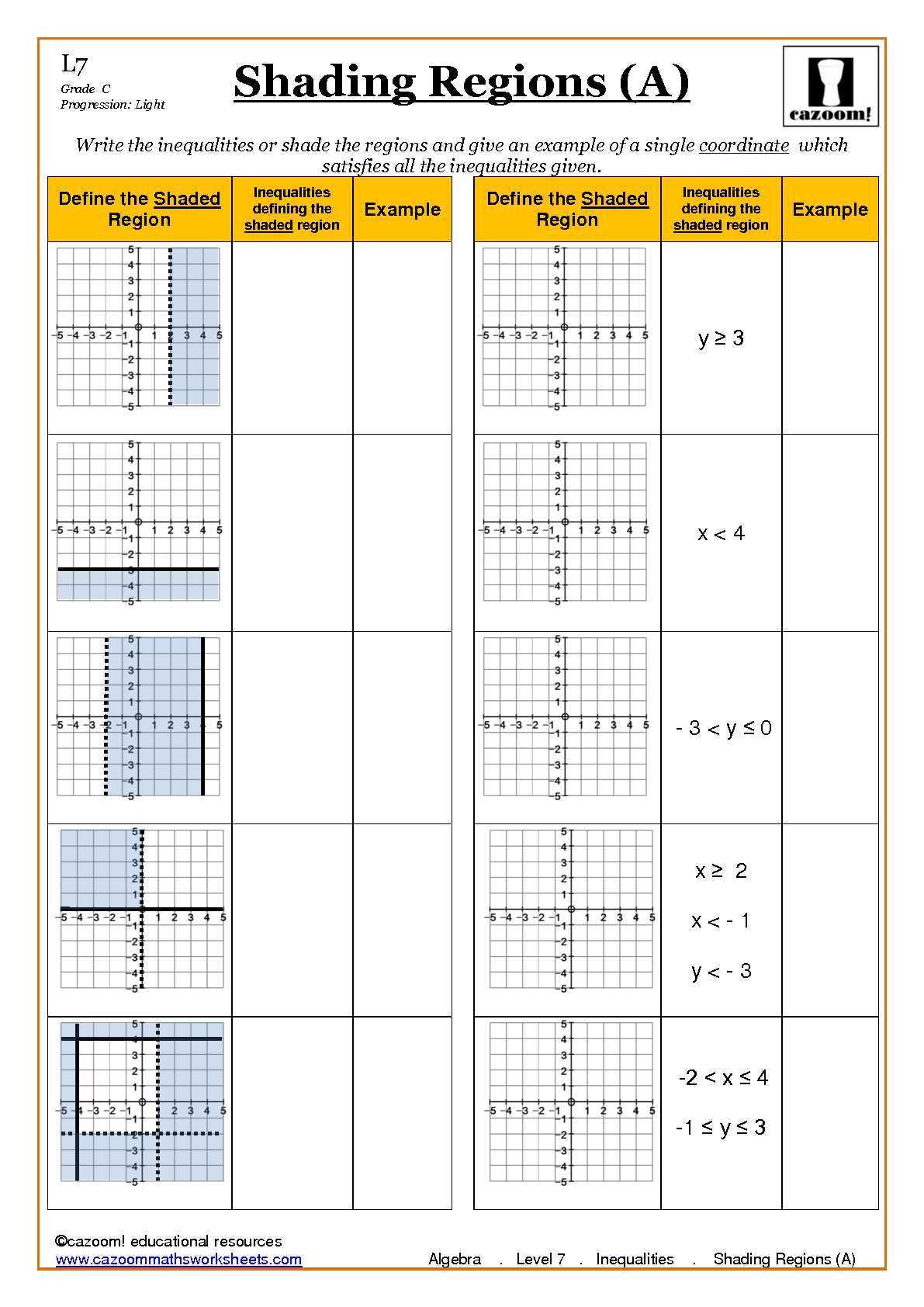
From the slope, you can find the curve that passes through the origin. You can use quadratic functions to calculate many different things, such as the area of a triangle. However, if you want to know the actual quadratic formula, you can use the quadratic formula which is listed below.
It’s easy to prove that a given quadratic function can be written in quadratic form. Using practice worksheets and graphing programs, you can use your knowledge of algebra to prove that a given quadratic function can be plotted in a quadratic form.