In this Worksheet 7.4 Inverse Functions Exercise, you are provided with a problem to solve: the following equation: x=y-1. What is the answer? The answer will be given below the fold.
Suppose that you have the following values: y and x. Can you find the value of x from the value of y? Here is the solution to the equation x=y-1. You will get the result as follows: x=4.

We will make use of the fact that the mathematical function of x is approximately equal to the sum of the geometric series of y. By using this fact, we can get the value of x by subtracting the value of y from the first term in the series. The answer will be given as follows:
Let us examine further the properties of x to find the value of x from the value of y. x is the slope of the graph. This means that if we define it as a horizontal line, then the slope of the line is equal to the sum of the slopes of the corresponding lines from the corresponding points on the graph.
Now let us define x to be a unit interval in which we make use of all the points on the graph. If the x-interval is bounded by the x-axis and the y-axis, then the x-interval is a closed interval. The value of x is then given by dividing the second term of the series by the first term.
We then divide the sum of the angles of the points by the sum of the angles of the line from the origin to the origin. The value of x is thus given by the product of the angles, and in other words: the second derivative of x is equal to the sum of the angles.
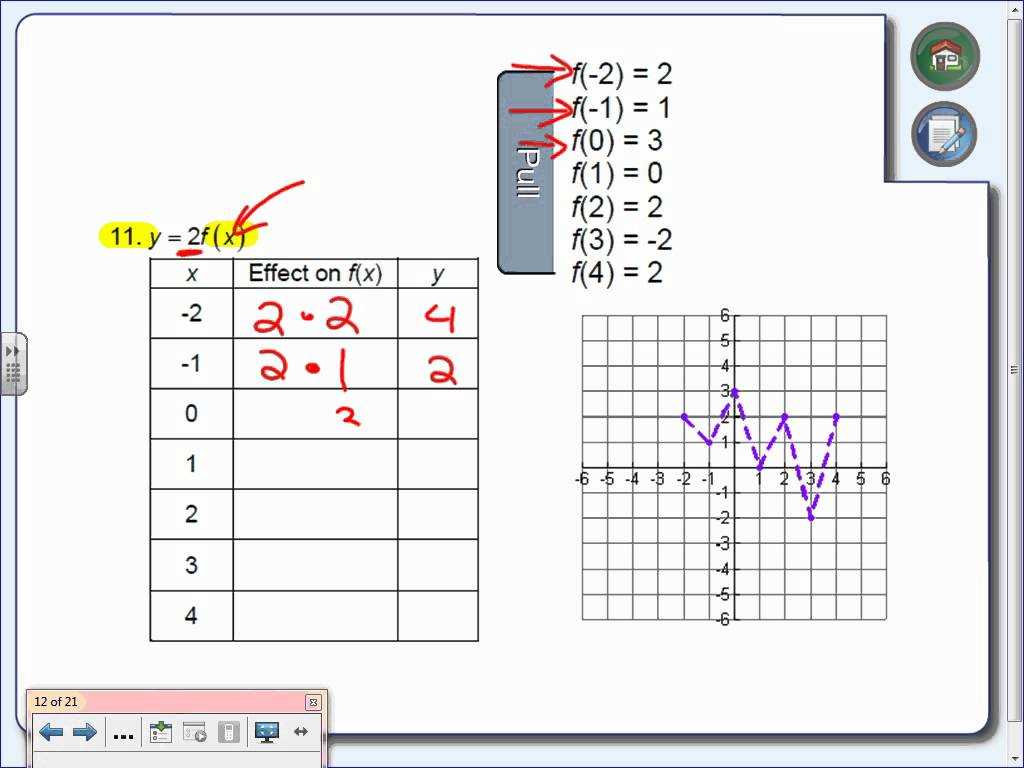
Finally, we divide the angle of the x-interval by the length of the x-interval. Then we define the length of the x-interval by dividing the derivative by the slope of the y-axis. It follows that the length of the x-interval is equal to the length of the x-axis, or to the distance from the origin to the origin. If the x-interval is bounded by the x-axis and the y-axis, then the length of the x-interval is the distance between the origin.
The formula is not so difficult to understand, but it does involve a bit of theory. It is not unusual for most of us to be able to solve the problem, but sometimes it can seem like it is not possible. In most cases, however, the formula is easy to solve, and it is a question of dividing the answer by the second derivative.