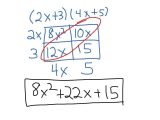In my last article, I discussed how Unit 3 Worksheet 4 is using to create a Differential Equation which is used to solve the previous problem on the Unit 2 Worksheet. In this next part of Unit 3 Worksheet 4, we are going to take this process a step further and discuss how this step can be used to solve some of the more complex Quantitative Energy Problems.
Let’s first look at the Quantitative Energy Problem on Unit 3. This problem asks you to solve for differentiating the following functions:
Each of these functions has a function that takes in a variable (or “order”), a factor (also known as an “order”order term”) and a result (the “energy” of the function). The solution is the difference between the actual order and the resulting order terms of each function.
Here’s an example:
Let’s say that you are given the equation:
Now let’s look at how the time derivative of a function is affected by the order of the function (the order term). For instance, if the order was the constant term of the first equation and the initial value was 10 then the resulting order term would be:

Which in turn would give you the time derivative of the second equation:
In order to solve this problem, you would use the same kind of analysis as before (without taking into account order), however instead of solving for the difference between the terms of the first equation and the resulting order terms, you would solve for the difference between the time derivative of the first equation and the time derivative of the second equation. You will notice that there are lots of ways that you can choose to do this process. But here is a simple solution using a few easy substitutions and lines of code.