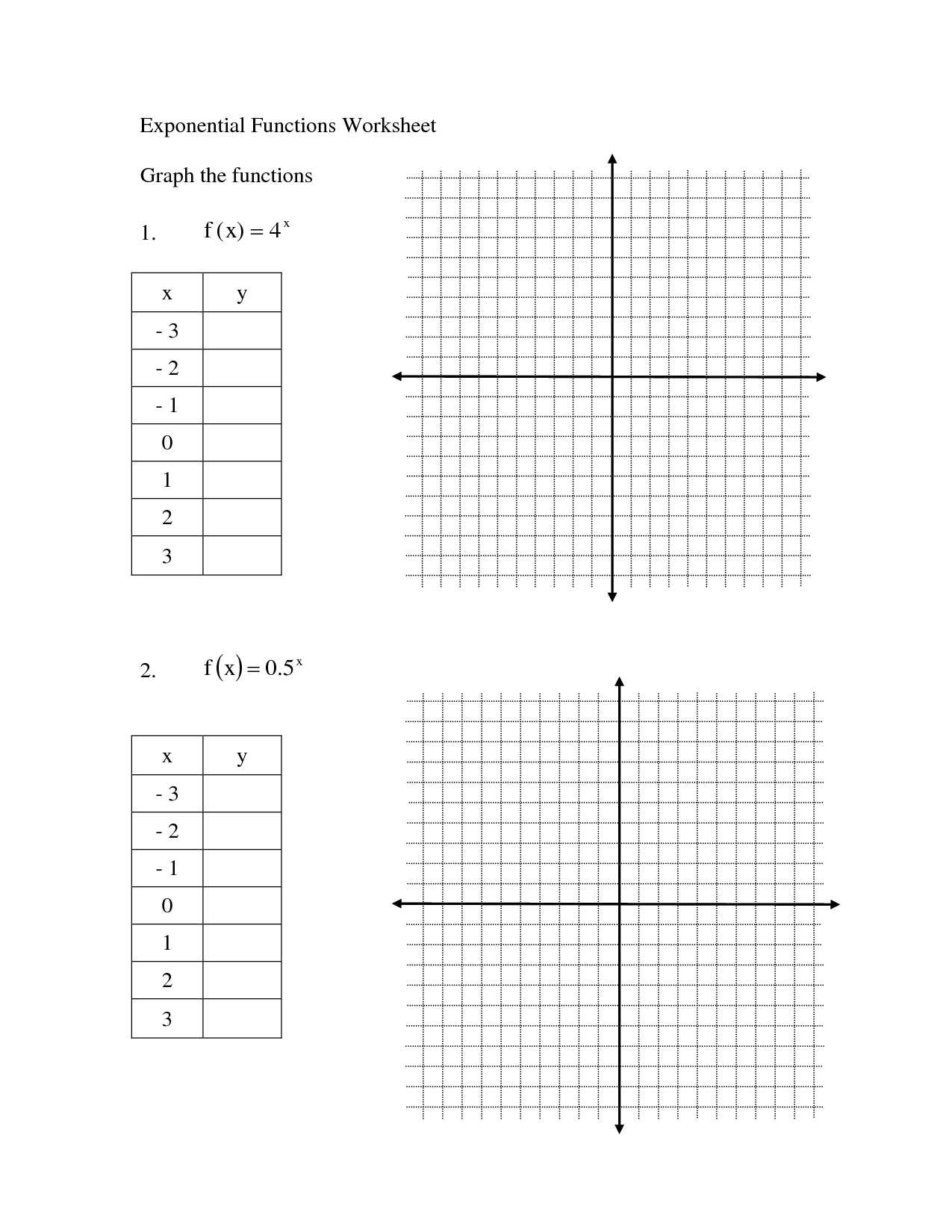
Solving Exponential Equations in a Worksheet will require the student to do three things in order to solve the equation properly. The first step is to calculate the Root Mean Square of the two points on the x-axis that affect the input and output of the equation. The second step is to select a scalar, and then determine if the product is positive or negative. Finally, if the product is negative, the next step is to find the factor that determines how high or low the input will be.
The products of the two factors in this case are -1. To calculate the RMS, divide the product by the total number of terms that will appear in the solution. This results in a value that can be used to find the factors. If there are not enough factors, then one of the constants must be substituted for the missing factor.
In order to find the factor, the x-coordinate is multiplied by the epsilon-function. The result is an angle from the plane. Use the angle to calculate the angle between the input and output points. This is the known factor.
By using the divisor of the unknown factor, the answer becomes in the same order as the unknown factor. That is, if the unknown factor is a positive number, it means that the input is high while the output is low. Thus, the unknown factor must be replaced with the value in the constant-variable form.
The division of the unknown factor by the epsilon-function can be calculated by subtracting the positive product from the epsilon-function. This will return the known value of the factor. However, if the factor is zero, then the answer will be a fraction, which is subtracted from one or the other variable in the equation to determine the answer.
If the answer is positive, then the factor must be replaced with the value that will represent the degree of freedom of the equation. Also, if the answer is negative, then the constant must be determined. The second step is to determine how high or low the output will be. In this case, the epsilon-function function does not exist and therefore can be used as the constant.

The values of the epsilon-function in Exponential Equations Worksheet are based on the outputs of the previous steps, which is why it is called a factor. The values are always rounded to the nearest integer. Using the G factor in Exponential Equations Worksheet can save the student from the trouble of finding the constant, which can be very difficult.
Using the log of the epsilon-function for the factor will also work well. This will reduce the opportunity for the student to make a mistake, since the exponents are always the same in every equation.