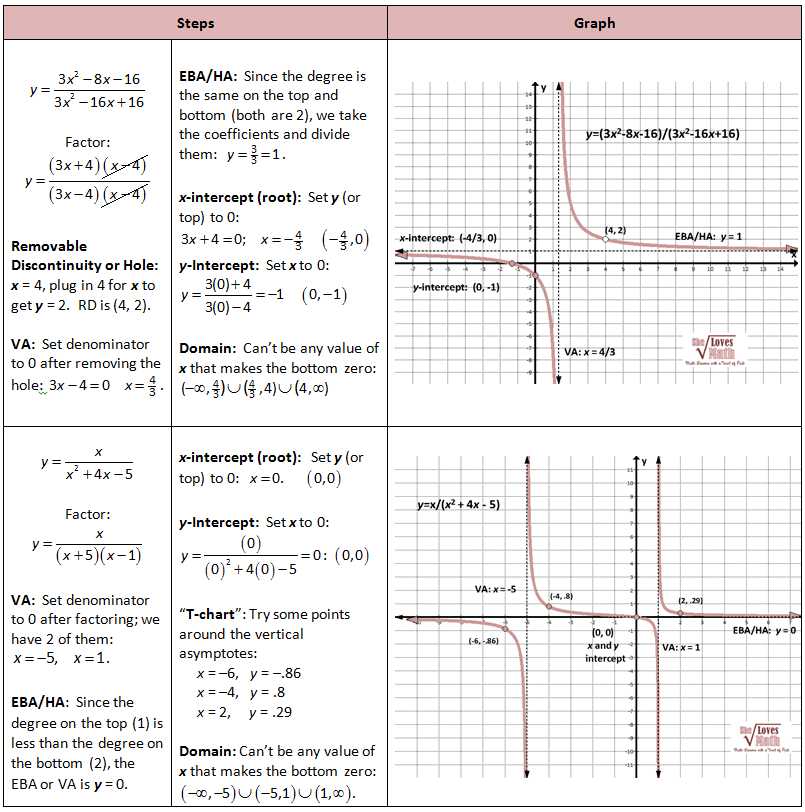
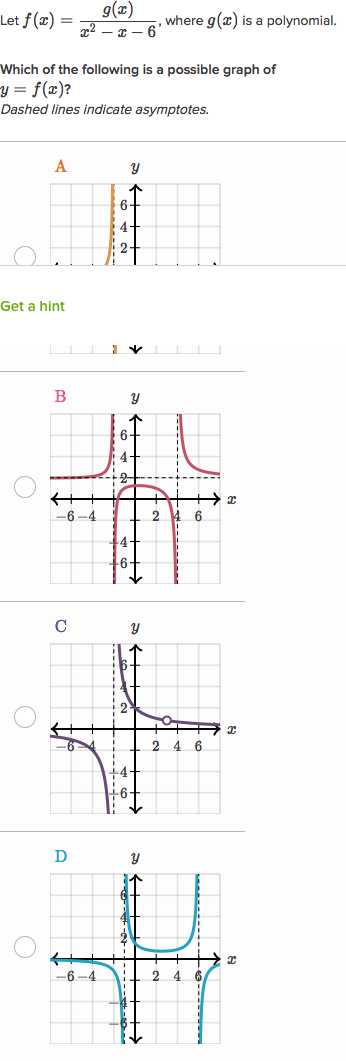
Graphical displays of graphing functions (otherwise known as Rational Functions) are a useful way to quickly evaluate problem solving capabilities. A graphing function is simply a formula that you can use to express the relationship between two variables, usually numerical. A graph of this formula can give you answers for many situations involving the relationship between the variables.
Graphing functions are commonly found in more advanced equations such as in combination with polynomials, and derivatives. The purpose of a graphing function is to describe the relationship between the x-intercept and y-intercept of a given function. There are a variety of different graphing functions available to you, and many of them have different applications than others.
The first kind of graphing function is the horizontal asymptote. These are often used to help with evaluating whether a function has a value at some point or not. If you draw a line through the two points where the desired value lies, then examine the end result you will see that it is either centered there, or in a horizontal plane. If it is centered, then you know that it will always be a value above the line, and if it is on a horizontal plane then you know that it will never be outside the plane.
Next is the vertical asymptote. These too are used to help you evaluate whether a certain function has a value when it is plotted on a particular graph. If the result of the function when plotted on a graph is outside the graph’s x-axis, then you know that it will never be a value below the graph’s x-axis. If it is outside the graph’s y-axis, then you know that it will never be a value above the graph’s y-axis.
The third kind of graphing function is the shape asymptote. This is used in conjunction with both the horizontal asymptote and the vertical asymptote. This particular type of graphing function is often used to determine if a certain function has a specific shape or form, and it is also used in solving non-integral equations.
There are many different types of graphing functions, and these can all be used for different purposes. Many of the graphs of these functions can help you in evaluating the situation being investigated. For example, you can use the value of a particular relationship to determine the probability that the outcome will occur in the next trial, or even the probability that it will occur at all. You can also use these graphs to help you evaluate your understanding of a given concept.

A great way to test out a graphing function is to set it up on the computer and analyze it directly. One popular way to do this is to download one of the many free graphing function programs. There are many functions out there, and each one should have a way to view the results for you on the screen of your computer. Once you have made your selection, you can start graphing.
You will be amazed at the ways in which analytical functions can be used to solve various problems. Of course, there are also real-world situations in which graphing functions are used to solve problems in other ways. Most of the time they are used for simplicity, but they can also be very valuable in other situations as well.