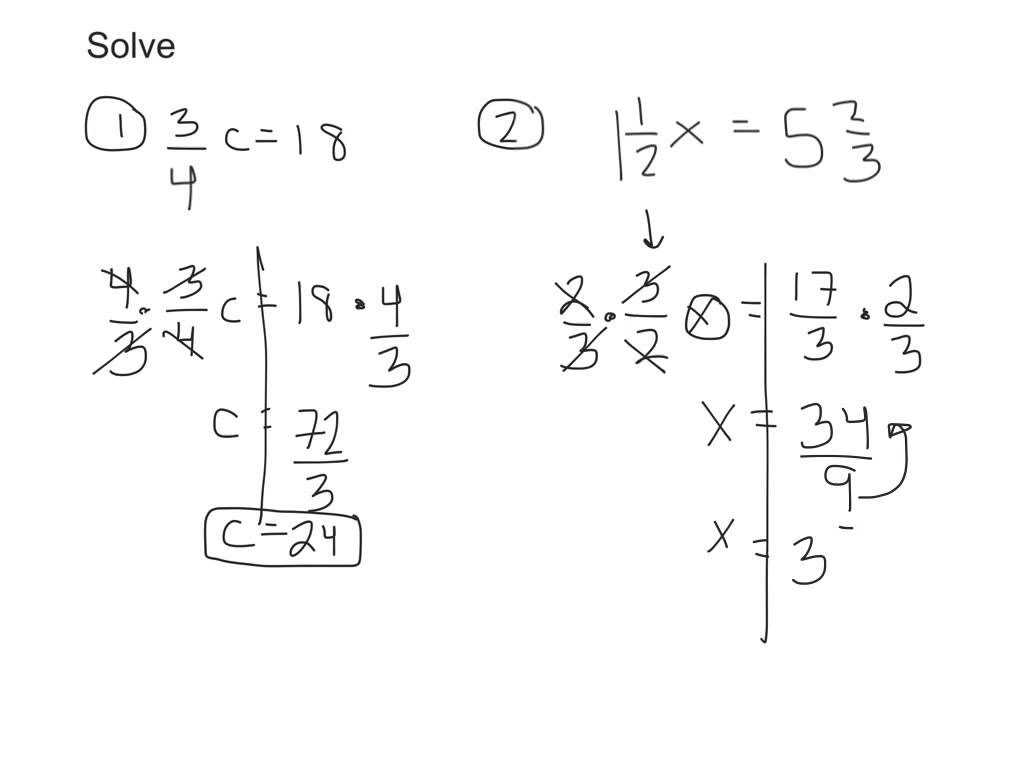Quadratic equations are a type of equation that has four variables. The most common form of the quadratic equation is the Parabola, which means “great circle” in Latin. This type of equation can be solved using methods including solving for the base and solving for the variable that has the largest value, commonly called the x-axis, or finding the best-fit line by factoring the unknown. In general, factoring quadratic equations involves solving for the coefficients of the right-hand side (or the left-hand side of the equation has four sides) and the unknown.
There are many ways to solve a quadratic equation. Two of the most commonly used methods are: firstly, solving the quadratic equation directly; and secondly, finding the solutions for the right-hand side. Using one or the other method, a quadratic equation can be evaluated in either of two different ways. The following quadratic worksheet answers will provide step-by-step directions for how to find the right answers for a quadratic algebra equation.
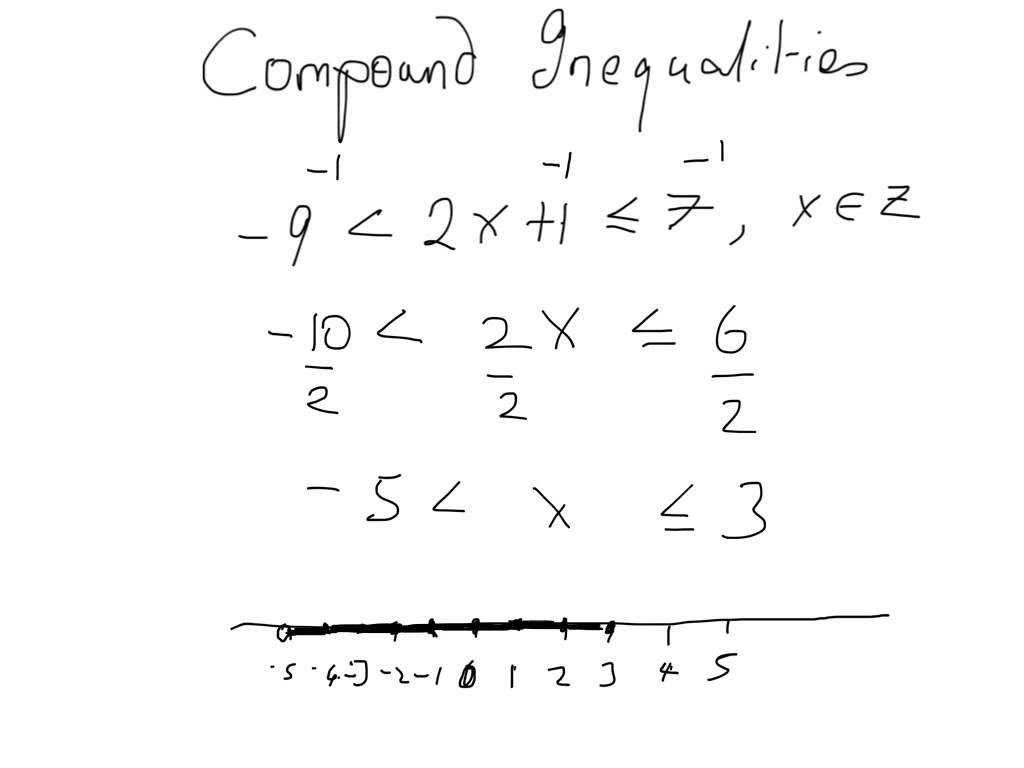
The first step in finding the right answer for an algebraic quadratic equation is to note the initial conditions on the quadratic equation. The two initial conditions that are commonly checked for are the fundamental constants, x, and y. The next step in finding the right answer for a quadratic equation is to solve for the variables of the equation.
The two initial conditions, x and y, must both be positive numbers. The resulting value of x will also be a positive number. If the values of x and y are not positive, the quadratic equation will result in a zero value for x. If the values of x and y are both positive, then the answer will be a positive number, and if either x or y is negative, then the answer will be a negative number.
The next step in finding the right answer for an algebraic quadratic equation is to find the solutions for the initial conditions. Finding the solutions for the initial conditions is done by factoring the unknown. A quadratic equation can have several unknowns, such as variables that have complex numbers as their initial conditions. Factoring the unknowns can be a bit tricky.
An example of how to find the solutions for a quadratic equation is to start with a formula for solving for x that has a simple solution. For this formula, the unknowns that are the initial conditions are a complex number, while the variables that are used to check the quadratic equation are a real number. From the formula for factoring, the variables that are multiplied together to get the real answer will end up as negatives, making the equation of a quadratic.

The formula for factoring a quadratic equation is x^2 +y^2 = z, where x and y are still both positive numbers. Then, the solution to the equation is z = f(x) x^2 + f(y) y^2, which is the most common form of factoring a quadratic equation. The quadratic equation can also be factored directly, so this method does not need to be used when factoring quadratic equations.
The steps for finding the right answer for an algebraic quadratic equation can be found by searching online for quadratic worksheets. Several of these are available, and each contains a variety of different quadratic worksheets, which can be solved using the same methods to find the right answers.